Allgemeine Informationen zu 3D Daten¶
Die folgenden Abschnitte beschreiben, wie Disparitätsbilder aus Stereobildpaaren berechnet werden, und wie Disparitäts-, Fehler- und Konfidenzbilder verwendet werden können, um daraus Tiefendaten und -fehler zu berechnen.
Berechnung von Disparitätsbildern¶
Nach der Rektifizierung haben das linke und das rechte Kamerabild die Eigenschaft, dass ein Objektpunkt in beiden Bildern auf die gleiche Pixelreihe projiziert wird. Die Pixelspalte des Objektpunkts ist im rechten Bild maximal so groß wie die Pixelspalte des Objektpunkts im linken Bild. Der Begriff Disparität bezeichnet den Unterschied zwischen den Pixelspalten im rechten und linken Bild und gibt indirekt die Tiefe des Objektpunkts, d.h. dessen Abstand zur Kamera an. Das Disparitätsbild speichert die Disparitätswerte aller Pixel des linken Kamerabilds.
Je größer die Disparität, desto näher liegt der Objektpunkt. Beträgt die Disparität 0, bedeutet dies, dass die Projektionen des Objektpunkts in der gleichen Bildspalte liegen und der Objektpunkt sich in unendlicher Distanz befindet. Häufig gibt es Pixel, für welche die Disparität nicht bestimmt werden kann. Dies ist der Fall bei Verdeckungen auf der linken Seite von Objekten, da diese Bereiche von der rechten Kamera nicht eingesehen werden können. Zudem lässt sich die Disparität auch bei texturlosen Bereichen nicht bestimmen. Pixel, für welche die Disparität nicht bestimmt werden kann, werden mit dem besonderen Disparitätswert 0 als ungültig markiert. Um zwischen ungültigen Disparitätsmessungen und Messungen, bei denen die Disparität aufgrund der unendlich weit entfernten Objekte 0 beträgt, unterscheiden zu können, wird der Disparitätswert für den letztgenannten Fall auf den kleinstmöglichen Disparitätswert über 0 gesetzt.
Um Disparitätswerte zu berechnen, muss der Stereo-Matching-Algorithmus die zugehörigen Objektpunkte im linken und rechten Kamerabild finden. Diese Punkte stellen jeweils den gleichen Objektpunkt in der Szene dar. Für das Stereo-Matching nutzt der rc_visard NG SGM (Semi-Global Matching). Dieser Algorithmus zeichnet sich durch eine kurze Laufzeit aus und bietet, insbesondere an Objekträndern, bei feinen Strukturen und in schwach texturierten Bereichen, eine hohe Genauigkeit.
Unabhängig vom eingesetzten Verfahren ist es beim Stereo-Matching wichtig, dass das Bild über eine gewisse Textur verfügt, durch Muster oder Oberflächenstrukturen. Bei einer gänzlich untexturierten Szene, wie einer weißen Wand ohne jede Struktur, können Disparitätswerte entweder nicht berechnet werden, oder aber die Ergebnisse sind fehlerhaft oder von geringer Konfidenz (siehe Konfidenz- und Fehlerbilder). Bei der Textur in der Szene sollte es sich nicht um ein künstliches, regelmäßig wiederkehrendes Muster handeln, da diese Strukturen zu Mehrdeutigkeiten und damit zu falschen Disparitätsmessungen führen können.
Für schwach texturierte Objekte oder in untexturierten Umgebungen lässt sich mithilfe eines externen Musterprojektors eine statische künstliche Struktur auf die Szene projizieren. Dieses projizierte Muster sollte zufällig sein und keine wiederkehrenden Strukturen enthalten. Der rc_visard NG bietet das IOControl-Modul als optionales Softwaremodul (siehe IOControl und Projektor-Kontrolle, das einen Musterprojektor ansteuern kann.
Berechnung von Tiefenbildern und Punktwolken¶
Die folgenden Gleichungen zeigen, wie sich die tatsächlichen 3D-Koordinaten \(P_x, P_y, P_z\) eines Objektpunkts bezogen auf das Kamera-Koordinatensystem aus den Pixelkoordinaten \(p_{x}, p_{y}\) des Disparitätsbilds und dem Disparitätswert \(d\) in Pixeln berechnen lassen:
wobei \(f\) die Brennweite nach der Rektifizierung (in Pixeln) und \(t\) der während der Kalibrierung ermittelte Stereo-Basisabstand (in Metern) ist. Diese Werte werden auch über die GenICam-Schnittstelle zur Verfügung gestellt (siehe Besondere Parameter der GenICam-Schnittstelle des rc_visard NG).
Bemerkung
Das Kamera-Koordinatensystem des rc_visard NG ist in Koordinatensysteme definiert.
Bemerkung
Der rc_visard NG stellt über seine verschiedenen Schnittstellen einen Brennweitenfaktor bereit. Er bezieht sich auf die Bildbreite, um verschiedene Bildauflösungen zu unterstützen. Die Brennweite \(f\) in Pixeln lässt sich leicht bestimmen, indem der Brennweitenfaktor mit der Bildbreite (in Pixeln) multipliziert wird.
Es ist zu beachten, dass für Gleichungen (1) davon ausgegangen wird, dass das Bildkoordinatensystem im Bildhauptpunkt zentriert ist, der üblicherweise in der Bildmitte liegt, und dass sich \(p_{x}, p_{y}\) auf die Mitte des Pixels bezieht, durch Addieren von 0.5 auf die ganzzahligen Pixelkoordinaten. In der folgenden Abbildung ist die Definition des Bildkoordinatensystems dargestellt.
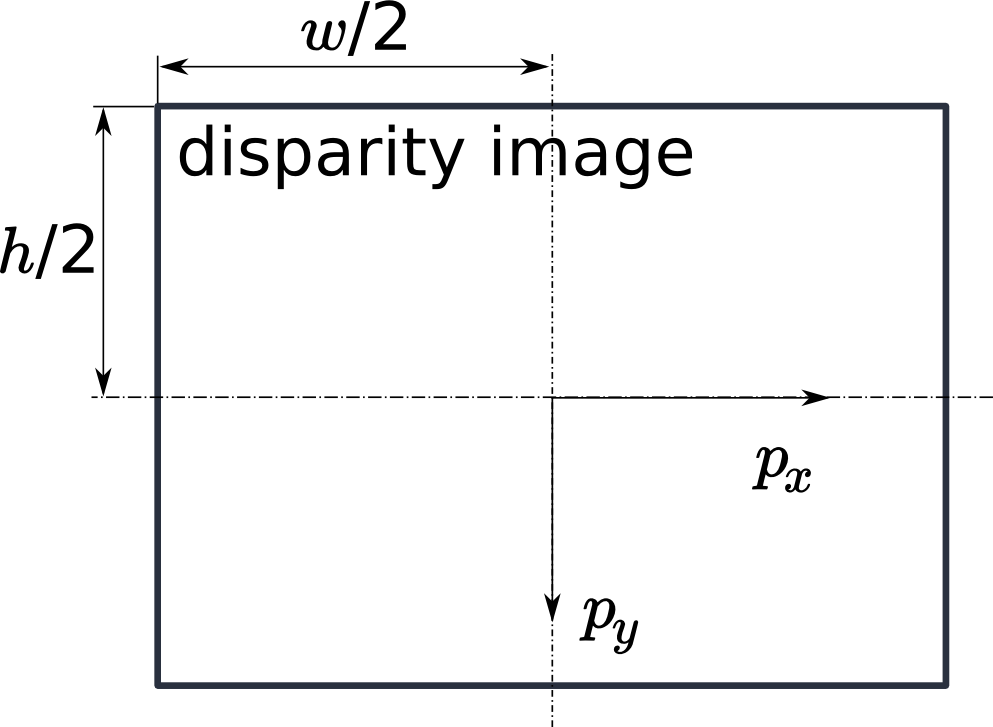
Abb. 15 Bildkoordinatensystem: Der Ursprung des Bildkoordinatensystems befindet sich in der Bildmitte – \(w\) ist die Bildbreite und \(h\) die Bildhöhe.
Die gleichen Formeln, aber mit den entsprechenden GenICam-Parametern, sind in Umwandlung von Bild-Streams angegeben.
Die Gesamtheit aller aus dem Disparitätsbild errechneten Objektpunkte ergibt eine Punktwolke, die für 3D-Modellierungsanwendungen verwendet werden kann. Das Disparitätsbild kann in ein Tiefenbild umgewandelt werden, indem der Disparitätswert jedes Pixels durch den Wert \(P_z\) ersetzt wird.
Bemerkung
Auf der Homepage von Roboception (http://www.roboception.com/download) stehen Software und Beispiele zur Verfügung, um Disparitätsbilder, welche über GigE Vision vom rc_visard NG empfangen werden, in Tiefenbilder und Punktwolken umzuwandeln.
Konfidenz- und Fehlerbilder¶
Für jedes Disparitätsbild wird zusätzlich ein Fehler- und ein Konfidenzbild zur Verfügung gestellt, um die Unsicherheit jedes einzelnen Disparitätswerts anzugeben. Fehler- und Konfidenzbilder besitzen die gleiche Auflösung und Bildwiederholrate wie das Disparitätsbild. Im Fehlerbild ist der Disparitätsfehler \(d_{eps}\) in Pixeln angegeben. Er bezieht sich auf den Disparitätswert an der gleichen Bildkoordinate im Disparitätsbild. Das Konfidenzbild gibt den entsprechenden Konfidenzwert \(c\) zwischen 0 und 1 an. Die Konfidenz gibt an, wie wahrscheinlich es ist, dass der wahre Disparitätswert innerhalb des Intervalls des dreifachen Fehlers um die gemessene Disparität \(d\) liegt, d.h. \([d-3d_{eps}, d+3d_{eps}]\). So lässt sich das Disparitätsbild mit Fehler- und Konfidenzwerten in Anwendungen einsetzen, für die probabilistische Folgerungen nötig sind. Die Konfidenz- und Fehlerwerte für eine ungültige Disparitätsmessung betragen 0.
Der Disparitätsfehler \(d_{eps}\) (in Pixeln) lässt sich mithilfe der Brennweite \(f\) (in Pixeln), des Basisabstands \(t\) (in Metern) und des Disparitätswerts \(d\) (in Pixeln) desselben Pixels im Disparitätsbild in einen Tiefenfehler \(z_{eps}\) (in Metern) umrechnen:
Durch Kombination der Gleichungen (1) und (2) kann der Tiefenfehler zur Tiefe in Bezug gebracht werden: