General information on 3D data¶
The following sections describe how disparity images are computed from stereo image pairs and how disparity, error and confidence images can be used to compute depth data and depth errors.
Computing disparity images¶
After rectification, an object point is guaranteed to be projected onto the same pixel row in both left and right image. That point’s pixel column in the right image is always lower than or equal to the same point’s pixel column in the left image. The term disparity signifies the difference between the pixel columns in the right and left images and expresses the depth or distance of the object point from the camera. The disparity image stores the disparity values of all pixels in the left camera image.
The larger the disparity, the closer the object point. A disparity of 0 means that the projections of the object point are in the same image column and the object point is at infinite distance. Often, there are pixels for which disparity cannot be determined. This is the case for occlusions that appear on the left sides of objects, because these areas are not seen from the right camera. Furthermore, disparity cannot be determined for textureless areas. Pixels for which the disparity cannot be determined are marked as invalid with the special disparity value of 0. To distinguish between invalid disparity measurements and disparity measurements of 0 for objects that are infinitely far away, the disparity value for the latter is set to the smallest possible disparity value above 0.
To compute disparity values, the stereo matching algorithm has to find corresponding object points in the left and right camera images. These are points that represent the same object point in the scene. For stereo matching, the rc_visard NG uses SGM (Semi-Global Matching), which offers quick run times and great accuracy, especially at object borders, fine structures, and in weakly textured areas.
A key requirement for any stereo matching method is the presence of texture in the image, i.e., image-intensity changes due to patterns or surface structure within the scene. In completely untextured regions such as a flat white wall without any structure, disparity values can either not be computed or the results are erroneous or have low confidence (see Confidence and error images). The texture in the scene should not be an artificial, repetitive pattern, since those structures may lead to ambiguities and hence to wrong disparity measurements.
When working with poorly textured objects or in untextured environments, a static artificial texture can be projected onto the scene using an external pattern projector. This pattern should be random-like and not contain repetitive structures. The rc_visard NG provides the IOControl module (see IO and Projector Control) as optional software module which can control a pattern projector connected to the sensor.
Computing depth images and point clouds¶
The following equations show how to compute an object point’s actual 3D coordinates \(P_x, P_y, P_z\) in the camera coordinate frame from the disparity image’s pixel coordinates \(p_{x}, p_{y}\) and the disparity value \(d\) in pixels:
where \(f\) is the focal length after rectification in pixels and \(t\) is the stereo baseline in meters, which was determined during calibration. These values are also transferred over the GenICam interface (see Custom GenICam features of the rc_visard NG).
Note
The rc_visard NG’s camera coordinate frame is defined as shown in Coordinate frames.
Note
The rc_visard NG reports a focal length factor via its various interfaces. It relates to the image width for supporting different image resolutions. The focal length \(f\) in pixels can be easily obtained by multiplying the focal length factor by the image width in pixels.
Please note that equations (1) assume that the coordinate frame is centered in the principal point that is typically in the center of the image, and \(p_{x}, p_{y}\) refer to the middle of the pixel, i.e. by adding 0.5 to the integer pixel coordinates. The following figure shows the definition of the image coordinate frame.
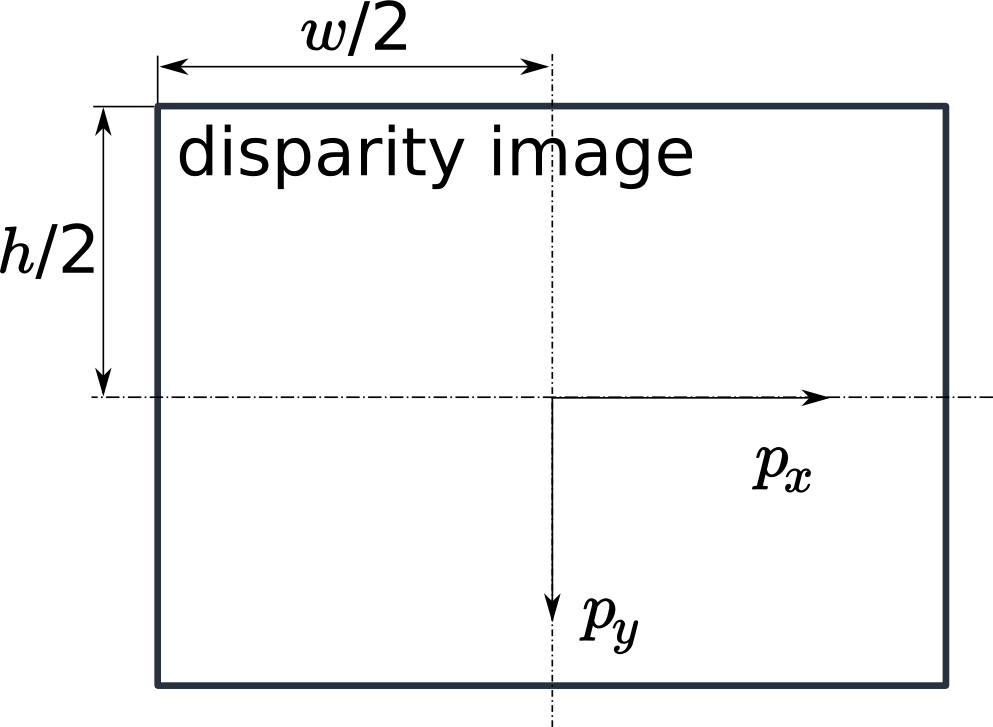
Fig. 15 The image coordinate frame’s origin is defined to be at the image center – \(w\) is the image width and \(h\) is the image height.
The same equations, but with the corresponding GenICam parameters are given in Image stream conversions.
The set of all object points computed from the disparity image gives the point cloud, which can be used for 3D modeling applications. The disparity image is converted into a depth image by replacing the disparity value in each pixel with the value of \(P_z\).
Note
Roboception provides software and examples for receiving disparity images from the rc_visard NG via GigE Vision and computing depth images and point clouds. See http://www.roboception.com/download.
Confidence and error images¶
For each disparity image, additionally an error image and a confidence image are provided, which give uncertainty measures for each disparity value. These images have the same resolution and the same frame rate as the disparity image. The error image contains the disparity error \(d_{eps}\) in pixels corresponding to the disparity value at the same image coordinates in the disparity image. The confidence image contains the corresponding confidence value \(c\) between 0 and 1. The confidence is defined as the probability of the true disparity value being within the interval of three times the error around the measured disparity \(d\), i.e., \([d-3d_{eps}, d+3d_{eps}]\). Thus, the disparity image with error and confidence values can be used in applications requiring probabilistic inference. The confidence and error values corresponding to an invalid disparity measurement will be 0.
The disparity error \(d_{eps}\) (in pixels) can be converted to a depth error \(z_{eps}\) (in meters) using the focal length \(f\) (in pixels), the baseline \(t\) (in meters), and the disparity value \(d\) (in pixels) of the same pixel in the disparity image:
Combining equations (1) and (2) allows the depth error to be related to the depth: